Liberty Instruments, Inc.
Reflecting on Echoes and the Cepstrum: A Look at Quefrency Alanysis and Hearing
(originally printed in Speaker Builder Magazine)
I read with great interest the article by Newell and Holland in the 8/94 issue of Speaker Builder, "Round the Horn" [1]. All in a single article were included a discussion of horns, an intriguing application of a relatively obscure digital signal processing technique called "cepstral analysis", and a reported link between the audible sound signature of driver types with a form of data measured from them.
Horns have always fascinated me. There is something very seductive in the complete effortlessness with which they can handle diverse levels, maintaining the same character from loud to soft. There is also an unusual sense of clarity often obtainable from horns. Unfortunately, coupled with their ability to sound the same at greatly differing levels is the horns’ reputation that the sound at all of these levels has not seemed particularly good. If only horns wouldn’t honk like that. And if only one could listen to a horn-based system without being constantly aware of the distinct existence of each horn driver. Horns are seldom admired for blending well.
I had read about the Cepstrum (an anagram of the word "spectrum") in various DSP texts, and about its use in voice speech synthesis and analysis. Dr. Holland’s use of the power cepstrum for investigating drivers was a new wrinkle. As a developer of loudspeaker measurement and analysis software (IMP, IMP/M and Liberty Audiosuite), I am in the fortunate position of being able to combine existing and newly developed procedures to relatively easily implement various analysis techniques as they become of interest. This development has resulted in inclusion of cepstral analysis capabilities in Liberty Audiosuite. (Note: this function is also provided as a PostProcess in PRAXIS).
A reported connection between similarity in cepstrum plots and similarity in sound character is interesting not only for the great promise it could have for developing better drivers. It also brings up intriguing questions about why the ear might be sensitive to the kinds of sound characteristics which register on a power cepstrum plot. At the end of this article I will offer a few conjectures, some analogues, and a wild hypothesis or two on this subject.
Disclaimer
Cepstral Analysis being a new subject to most readers, there will inevitably be many questions and some difficulty in understanding the concepts. But please do not assume that I am an expert on this subject, on horns, or on the theory of hearing. In all cases, your author is in the position of student and this article should be read as from one sharing his notes, not from a final authority in these fields. I recommend that the sited references be counsulted directly for more concrete information!
Welcome to the Quefrency Domain
The terminology surrounding the computation of the cepstrum came from the original article by Bogert et al [2], in which various terms from signal processing (spectrum, frequency, phase, analysis) were rearranged into anagrams (cepstrum, quefrency, saphe, alanysis). The authors did this to highlight the unusual treatement of frequency domain data as if it were time domain data in generating a new data set which had across its x-axis values (the quefrencies) in units of seconds but which indicated variations in the frequency spectrum. Evidently, only the term "cepstrum" remains in common use, but I prefer to retain at least the term "quefrency" to remind me that the seconds shown on the plots aren’t time as I might normally consider it.
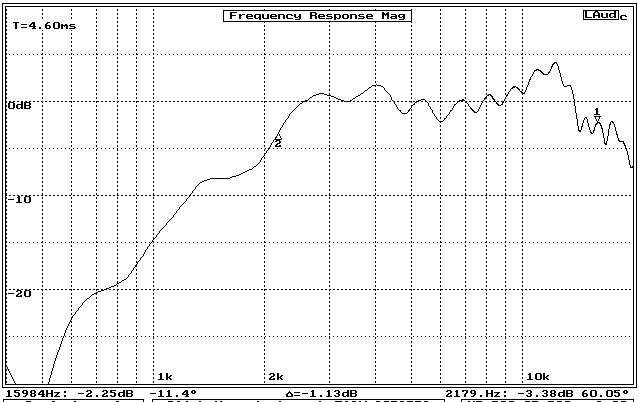
What is this power cepstrum stuff all about? In simple terms, the power cepstrum is a measure of the periodic wiggliness of a frequency response plot. Users of PRAXIS, IMP and Liberty Audiosuite have no doubt noticed that the frequency response curves of their speakers often have sinewave-like ripples superimposed on the general shape. This will be particlularly noticeable if the response measurement includes a distinct reflection from a wall, grille or cabinet edge. An example is shown in figure 1, for which a large cardboard reflector was placed 12 inches from a horn tweeter prior to the measurement.

Figure 1: Frequency Response of round horn when strong echo (reflection) is included (notice the ripples in the curve)
An equivalent measurement made without the reflector is shown in figure 2. Why should a reflection generate response ripples?
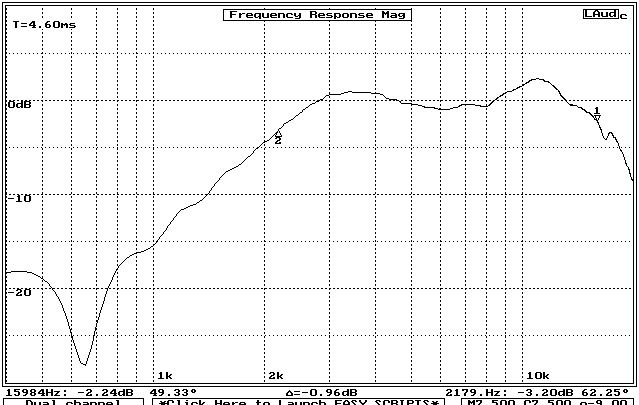
Figure 2: Frequency Response of same horn without reflections
By Fourier’s theorem, we know that signals can be represented mathematically as an infinite collection of sinewaves of various frequencies, magnitudes and phases. The idea of a frequency response plot for a system is based on this concept, showing the output magnitudes and/or phases corresponding to the sinewaves of each frequency if all were applied at the input at equal levels and phase aligned.
When a speaker emits a signal, this is equivalent to an emission of a collection of sinewaves. When this signal bounces off something else, or is emitted a second time shortly thereafter by the speaker, two such sinewave collections arrive at the measuring microphone together but offset in time. At each sinewave frequency, if the pair arrive exactly in phase, their amplitudes add. If they arrive exactly in reverse phase, the amplitudes subtract and will even cancel completely if the arriving amplitudes are equal. Phase differences between these extremes will cause less intense levels of reinforcement or cancellation.
The phase and amplitude of the sinewave resulting from the combination of two arriving sinewaves of identical frequency will depend on two factors: the delay between the arrivals and the frequency. This is illustrated in figure 3, in which one packet of three sinewaves is shown offset in time relative to an identical packet of three sine waves. In the lower part of the figure the relative pressure value of the waves (vertical center of each wave being 0) at each frequency have been combined to form a resulting sinewave at that same frequency. The arithmetic is done for each frequency separately. For a given delayed second arrival time, the resulting sinewave amplitudes will vary periodically with increasing frequency, giving rise to response ripples as shown in figure 1.
The rate of the ripple variation appears to increase with frequency in figure 1 because the graph is in log-frequency format. Were the plot to be displayed in linear frequency format (i.e., equal number of Hertz per horizontal inch), the ripples would appear at a more steady rate.
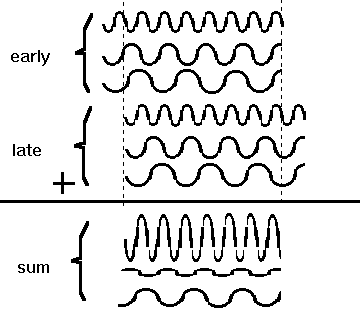
Figure 3: Sum of delayed sinewave packets
These variations are viewed in IMP and Liberty Audiosuite on a log-magnitude (dB) scale, which enhances the sinusoidal appearance of the ripples. In a scalar magnitude format, the shape would tend to look more like periodic notches taken out of the curve.
If you remember that the FFT of a sinusoidal time domain trace results in a peak at the sinusoid’s frequency, you can then imagine that an FFT of the log-magnitude frequency domain trace would result in peaks at the frequency response ripple rates. And these rates (in units of "per Hertz", i.e., seconds) are related to the delay times between the multiple arrivals of echoes. We get a display which is more or less that of echo intensity vs. delayed arrival time.
And of what good is that? First, it can be used to find, via the reported delay times, which baffle features might be causing the most dominant reflections and contributing to response errors or to debug quasianechoic measurement setups intended for loudspeakers. Second, it can be used to evaluate, design or modify drivers or horns by providing a window into the way waves are bounced around on the cones, diaphrams or horn necks. Perhaps most important, the process of cepstral analysis may have some similarities to the way hearing works and to the sorts of sound characteristics to which we are sensitive.
Processing Tricks
One major problem in a mere FFT of the response shape is that the abrupt changes at the response extremes, coming from A/D filtering, noise, and AC coupling capacitor effects, were strong enough to overwhelm any resolution of more subtle details. This is similar to the spectral leakage effect which can occur when a time domain data curve is truncated in IMP or LAUD, and the fix is also similar: use a "window" on the data to taper the edges to a midpoint value (zero). Further, at frequencies where a driver or speaker’s response is weak, noise will cause significant peak-to-peak dB variations which can dominate the result. Since we are probably less concerned with response ripples where the level is relatively low, this can be dealt with by further weighting the response curve via an envelope which emphasizes the ripples in higher output regions of the spectrum.
This windowing and weighting deals well with the abrupt edges and noise in a measured response. However, the shape of the resulting curve still tends to be dominated by the response rolloffs at the upper and lower ends of the drivers' frequency response. It will in general be useful to be able to minimize the contribution of this shape to the cepstrum curve so that finer details are not swamped out. A "hpFilter" (high-pass) option is implemented in the Liberty Audiosuite cepstrum facility to allow empasis of the higher quefrency ripples and remove the more gradual shapes resulting from normal driver rolloffs. Because of the better resolution at mid and higher quefrencies, this hpFilter was left on during the generation of the remaining plots in this article.
There is an additional switch in Liberty Audiosuite allowing you to select whether to include or ignore the "negative frequencies" of the source frequency response data. Although negative frequencies may sound like science fiction (or the result of really good bass response), a Fourier transform normally provides data values for frequencies which are below zero. For real world signals, these are always of the same magnitude (but of inverted phase) as for the corresponding positive frequency, so they are normally ignored in audio analysis. But in forming the Power Cepstrum, inclusion of negative frequency data has a strong effect on the graph. I usually choose to not include them as their effect has seemed to complicate efforts to relate the features of the plot to physical parameters which is already a challenging task in most cases.
The end result of performing Cepstrum Analysis (using the hpFilter and not using negative frequencies) on the curve of figure 1 is shown in figure 4.
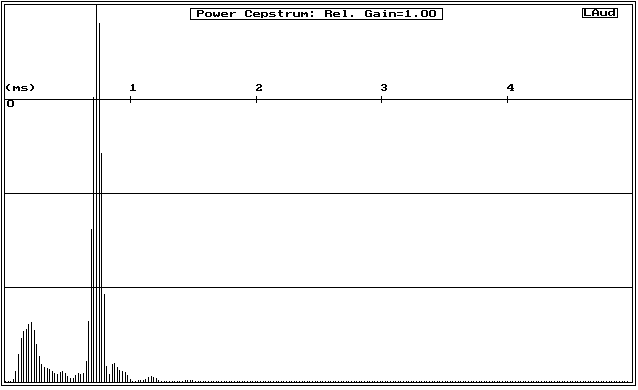
Figure 4: Power Cepstrum plot of data from Figure 1 (with reflection)
As stated earlier, the original response measurement for this was made using a large reflector to introduce a strong intentional echo into a measurement of a short axisymettric tweeter horn. Compare the cepstrum of figure 4 to that in figure 5, which is the equivalent cepstrum for the no-reflector data of figure 2. The peak due to the reflection(s) is very prominent.
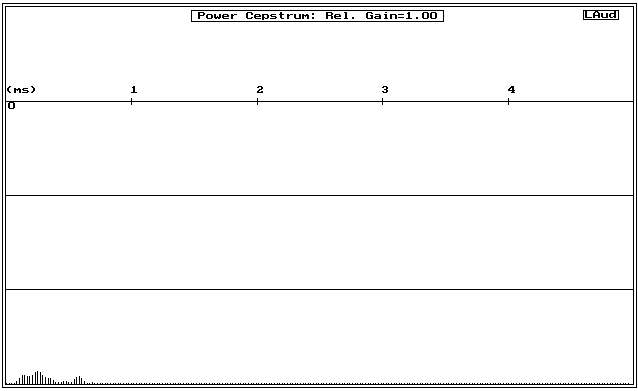
Figure 5: Power Cepstrum plot of data from Figure 2 (without reflector)
Some Measured Horn Effects
The horn used here is a 6 inch diameter, axisymmetric, home-made fiberglass unit, fabricated on a mold lathed from maple hardwood and generously waxed. A round piece of fiberglass circuit substrate (with the copper removed) was cut and drilled to allow mounting of a 1" Audax titanium dome tweeter (the driver). A 1.1" diameter hole was made on this piece to provide clearance for the dome and to serve as the horn throat. This was sanded and mounted onto the narrow end of the horn mold. Then resin-soaked fiberglass cloth was applied in 3" by 0.5" strips until the entire bell was covered with a thick layer, also bonding the driver mount board to the horn. When this hardened, it was pried from the mold, sanded, and painted with a black polyurethane paint. While more than an afternoon project, the operation was not as difficult as you might imagine. The resulting tweeter has proved very satisfactory in listening tests and is being used to provide the higher frequencies in a prototype 9-dB enhancement Focused Array speaker system (see "Focused Arrays" in SB ?/95).
Whereas the tweeter, when operated as a direct radiator, had a somewhat rising on-axis response, on the horn it had a falling response. For the measurements provided here, the horn loaded implementation is flattened by a simple resistor-capacitor network. For all cepstrums, the responses were first gain adjusted so that the main flat-response region of the spectrums were near the 0 dB line (the Liberty Audiosuite cepstrum analysis process applies the dB display gain before calculating).
Centered in the same location of an identical cardboard baffle board as for the horn measurements, the direct radiating response of this tweeter was measured at the same distance from the baffle, with the response shown in figure 6.
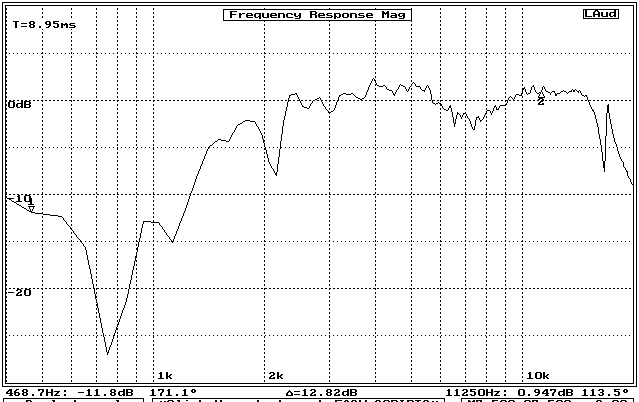
Figure 6: Response of same dome tweeter, as direct radiator (without horn), on same baffle
The cepstrum of the direct radiator measurement is shown in figure 7. Note that the scale of this plot is altered to utilize a display gain of 10, to better show the cepstral features.
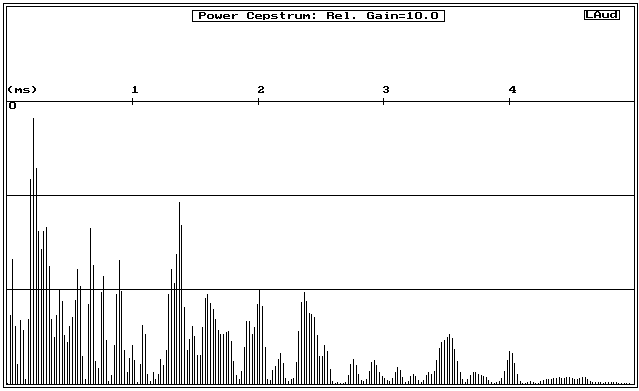
Figure 7: Power Cepstrum corresponding to data in figure 6 (dome as direct radiator, 10x display gain used)
For comparison, Figure 8 shows the power cepstrum at the same 10x scale for the horn data from figure 2.

Figure 8: Same as Figure 5 (horn), with 10x display increase
The direct radiator’s cepstrum shows more and stronger apparent reflections and at greater delays (i.e., higher "quefrencies"). Because of the small size of the tweeter dome which couldn’t easily support long delay times, it would seem that some of these reflections might be coming from the baffle edges. Holland suggests that some of the Cepstral features may be due to resonances and mechanical mismatches in a drivers’ construction, yielding results similar to those caused by reflections. The actual reflections are probably stronger for the direct radiator than for the horn because the horn’s directivity prevents significant energy from ever reaching the baffle edges. If such reflections are indeed audible and harmful to fidelity, a good case could be made against the often promoted desirability of achieving wide dispersion. If reflections are to be avoided, it would seem wiser to direct energy toward a fixed listening position and avoid spraying the edges of the cabinet or the listening room with sound energy.
Can You Hear a Cepstrum?
If, as is reported by Newell and Holland, the cepstral data is a significant indicator of the perceived character of a speaker, what could be the biological reason or explanation for this? It would certainly add to the plausiblity of the idea if a survival-related benefit to cepstral sensitivity existed and a physical means could be conceived by which cepstral information might be perceptible.
A key may be found in the nature of the human voice. I think it can be agreed that our ears are likely to be well adapted toward discerning the sonic character of voices. While the consonants of speech are usually transient and of short-burst character, vowel sounds (and tones sung by a singer) are formed by repetitive emission of pulses into the vocal tract [4]. The emitted pulses will be wideband in nature and the vocal tract will impart a frequency shaping to the overall output. But notice that this is again a short-term multiple emission of spectra (sinewave packets) similar to what may result from multiple reflections of broadband signals.
Sometimes a harmonic rich tone can actually be missing the fundamental, but the fundamental can still be distinctly "heard" [5] by the ear. The fundamental is not only the lowest tone present in a harmonic series, it is also the frequency spacing between the many harmonic multiples, which would appear as a cepstral peak whether the fundamental were truly present or not. Note also that cepstral analysis is essentially immune to phase response, as many tests indicate the ear may be; in the power cepstrum the effects of superimposed delayed responses are detectable in the response magnitude variations rather than via the phase components themselves.
Coming back to a previous topic (see "Focused Arrays" in SB ?/95), people are known to be sensitive to echo content in an acoustical environment. A listener may not be able to make a blindfolded identification between some brands of speakers in a room into which he has been led, but the same blindfolded listener would very likely be able to make a fair estimate of the size and wall placement of the room itself (this would make the basis of an interesting experiment if anyone is in need of a research project).
There are some plausible biological and survival-related reasons for such hearing abilities. In darkness, it could be useful to know by listening how far you, your prey, or an enemy may be, from a boundary or escape route. The quantity and distribution of delayed reflections could give clues to how far away an unseen sound source may be behind you. The audibility of reflections is easy to demonstrate even without test equipment. Listen to your voice as you read this sentence out loud to yourself in the middle of a room and then repeat it within two feet of a wall or table surface; a sound difference is unmistakable.
It is no far-fetched idea that biological apparatus could be able to extract spatial information from detected echoes. Bats have such well-developed echolocation that they use it in preference to vision. Perhaps a scaled down version of this ability in people is the source of some of the unconvincing sound fields often coming from hifi systems. With all the reproduced signal coming from one of two sound points, a twenty-piece orchestra could give a loudspeaker-induced echo pattern indicating that all of its twenty pieces are at the same spoint in your room!
Another proposed experiment (this for those more well equipped with hardware): Configure a general purpose digital signal processor as a filter to introduce response variations to recorded music, to be auditioned via headphones. If the ear is indeed sensitive to cepstral content then the presence of the filter, for the same slight peak-to-peak decibel variation, should be more audible when the variations are periodic (in frequency) than when they are random as a function of frequency.
Ultimate Reverse Engineering
Given that there might be good reasons for and some evidence that our hearing is sensitive to cepstral content, how might such processing be accomplished? Probably there is no internal A/D converter and two-tiered FFT process running in our brains to form the time domain waveform, the frequency response and then the cepstral response. How then might "periodic wiggles in the spectrum" be detected?
In a fascinating and highly-recommended article [5] "Hearing it Like it Is: Audio Signal Processing the Way the Ear Does It", Robert H. McEachern describes a system of human hearing, based on banks of bandpass filters (the ear is known to use sensitive hairs placed along a resonant structure, providing multiple-tuned bandpass characteristics). By comparing the ratios of the log-magnitude of energy detected in two such adjacent bandpass structures, both frequency and level can be accurately determined.
By doing this between multiple filter pairs tuned to different sets of center frequencies, multiple detections of an input are accomplished. This scheme is particularly well suited for detecting harmonically related tones and matching them via their similarly scaled frequency modulations so as to recognize them as coming from a single source. Thus a voice can provide the ear with wideband redundant information to provide immunity to interference: if one set of tones is masked by interference or by the cancellation effects, duplicate information content is obtainable via one of the other harmonics. This works even if the fundamental is missing entirely. Further, by this matching, multiple sounds can be sorted and differentiated (as in the "cocktail party effect") by recognizing the harmonic sets. McEachern hypothesizes that the ear may use this sensing and evaluation scheme using vowel tones (relatively narrowband) to sort out "channels" (frequency ranges) to be emphasized or desensitized in reception and interpretation of the wider band consonants, which carry the bulk of speech information.
This ability to detect and sort harmonically related tones seems very similar to what would be required to detect ripples in a broad spectrum modified by echoes. In both cases, periodic log magnitude changes in spectrum as a function of frequency, similar to cepstral data, is key. The separated frequency peaks caused by reflection of a broadband signal would not carry the common frequency modulation which would cause the ear to group the peaks together. But a hearing mechanism which identifies non-grouped periodic spectrum peaks for purposes of detecting interference might also make further use of such an ability for extracting information about the space around a sound source.
At some level, there is no doubt in my mind that echo patterns present the ear with clues about the three-dimensional environment in which a sound field exists. Whether this characteristic is best identified and analyzed in terms of a power cepstrum or by some other technique is yet to be determined. But reproducing the echo patterns of an original recording environment and not that of the listening room (or those generated by loudspeaker cabinets or mimicked by driver colorations) is an area of speaker design likely to keep many of us busy for a while.
References:
1. P. Newell and K. Holland, "Round the Horn", Speaker Builder, 8/94, pp 24-64.
2. B.P. Bogert, M.J. R. Healy and J.W. Tukey, "The Quefrency Alanysis of Time Series for Echoes: Cepstrum, Psuedo-Autocovariance, Cross-cepstrum and Saphe Cracking", Proceedings of the Symposium on Time Series Analysis, M. Rosenblat, Ed., Wiley, NY, 1963, pp 209-243.
3. K.R. Holland, "The Use of Cepstral Analysis in the Interpretation of Loudspeaker Frequency Response Measurements", Proceedings of the Institute of Acoustics, Vol. 15 Part 7, 1993, pp 65-71.
4. A.V. Oppenheim and R.W. Schafer, Discrete-Time Signal Processing, section 12.9 "Applications to Speech Processing", Prentice Hall, Englewood Cliffs, NJ, 1989, pp. 815-825.
5. R.H. McEachern, "Hearing It Like It Is: Audio Signal Processing the Way the Ear Does It", DSP Applications, February 1994, pp 35-47. [Golden Gate Enterprises: phone (415) 969-6920]